题目链接

转载自 walker

前置知识

• 假设 $x$ 能唯一分解为 ${p_1}^{e_1}{p_2}^{e_2}\dots {p_k}^{e_k}$，莫比乌斯函数 $\mu (x)$ 定义为：

$$\mu (x)=\{\begin{array}{l}\begin{array}{rl}0& ,\mathrm{\exists }{e}_i>1\\ 1& ,k\text{是偶数}\\ -1& ,k\text{是奇数}\end{array}\end{array}\text{或}\mu (x)=\{\begin{array}{l}\begin{array}{rl}1& ,n=1\\ (-1{)}^k& ,n=p_1{p}_2\dots p_k\\ 0& ,\text{其他}\end{array}\end{array}$$

题目分析

给定 $a,b,d$，求满足 $1\le x\le a,1\le y\le b$，并且 $gcd(x,y)=d$ 的数对 $(x,y)$ 个数 等价于 求满足 $1\le x^{\prime }\le \lfloor {\displaystyle \frac{a}{d}}\rfloor$，$1\le y^{\prime }\le \lfloor {\displaystyle \frac{b}{d}}\rfloor$，并且 $gcd(x^{\prime },y^{\prime })=1$ 的数对 $(x^{\prime },y^{\prime })$ 个数，即求两个区间内有多少对这样的数对是互质的。

证明：假设 $gcd({\displaystyle \frac{x}{d}},{\displaystyle \frac{y}{d}})>1$，那么 $gcd(x,y)>d$，矛盾。

可以用容斥原理求解，设 $\lfloor {\displaystyle \frac{a}{d}}\rfloor =a^{\prime }$，$\lfloor {\displaystyle \frac{b}{d}}\rfloor =b^{\prime }$ ，接下来统计不合法的对数：

有一个质公因子的方案数量：

$$\lfloor {\displaystyle \frac{a^{\prime }}{2}}\rfloor \cdot \lfloor {\displaystyle \frac{b^{\prime }}{2}}\rfloor +\lfloor {\displaystyle \frac{a^{\prime }}{3}}\rfloor \cdot \lfloor {\displaystyle \frac{b^{\prime }}{3}}\rfloor +\lfloor {\displaystyle \frac{a^{\prime }}{5}}\rfloor \cdot \lfloor {\displaystyle \frac{b^{\prime }}{5}}\rfloor +\cdots$$

有两个质公因子的方案数量：

$$\lfloor {\displaystyle \frac{a^{\prime }}{2\times 3}}\rfloor \cdot \lfloor {\displaystyle \frac{b^{\prime }}{2\times 3}}\rfloor +\lfloor {\displaystyle \frac{a^{\prime }}{2\times 5}}\rfloor \cdot \lfloor {\displaystyle \frac{b^{\prime }}{2\times 5}}\rfloor +\cdots$$

有三个质公因子的方案数量：

$$\lfloor {\displaystyle \frac{a^{\prime }}{2\times 3\times 5}}\rfloor \cdot \lfloor {\displaystyle \frac{b^{\prime }}{2\times 3\times 5}}\rfloor +\cdots$$

所以根据容斥原理，合法方案数为：

$$\begin{array}{rl}ans& =a^{\prime }b-\lfloor {\displaystyle \frac{a^{\prime }}{2}}\rfloor \cdot \lfloor {\displaystyle \frac{b^{\prime }}{2}}\rfloor -\lfloor {\displaystyle \frac{a^{\prime }}{3}}\rfloor \cdot \lfloor {\displaystyle \frac{b^{\prime }}{3}}\rfloor -\cdots \text{(只含一个质公因子)}\\ & +\lfloor {\displaystyle \frac{a^{\prime }}{2\times 3}}\rfloor \cdot \lfloor {\displaystyle \frac{b^{\prime }}{2\times 3}}\rfloor +\cdots \text{(只含两个质公因子)}\\ & -\lfloor {\displaystyle \frac{a^{\prime }}{2\times 3\times 5}}\rfloor \cdot \lfloor {\displaystyle \frac{b^{\prime }}{2\times 3\times 5}}\rfloor -\cdots \text{(只含三个质公因子)}\end{array}$$

注意到符号项就是莫比乌斯函数，故合法方案数可用莫比乌斯函数表示：

$$ans=a^{\prime }{b}^{\prime }+\sum _{i=2}^{min\{a^{\prime },b^{\prime }\}}\lfloor {\displaystyle \frac{a^{\prime }}{i}}\rfloor \cdot \lfloor {\displaystyle \frac{b^{\prime }}{i}}\rfloor \cdot \text{mobius}[i]$$

注意，$1\sim x$ 中因子 $d$ 的个数就是 $\lfloor {\displaystyle \frac{x}{d}}\rfloor$ 个，不仅只有质因子有这样的性质

如果直接枚举 $i$，由于 $a^{\prime },b^{\prime }\le 5\times {10}^4$，复杂度是 $O(n)$ 级别，并且询问个数有 ${10}^5$，直接枚举是 $O(n^2)$ 级别，考虑优化。

我们发现，这个式子理论上 $i$ 最多需要枚举 $N$ 次，但实际上因为整除的缘故，有很多 $i$ 对应的 $\lfloor {\displaystyle \frac{a^{\prime }}{i}}\rfloor$ 和 $\lfloor {\displaystyle \frac{b^{\prime }}{i}}\rfloor$ 都是相同的，所以是冗余枚举。由于 $i$ 从小到大枚举，$\lfloor {\displaystyle \frac{a^{\prime }}{i}}\rfloor$ 都是单调递减的，并且理论上只有 $2\sqrt{a}$ 个不同的值（$\lfloor {\displaystyle \frac{b^{\prime }}{i}}\rfloor$ 同样）。这里用到了 AcWing 199. 余数之和 中的知识。

---

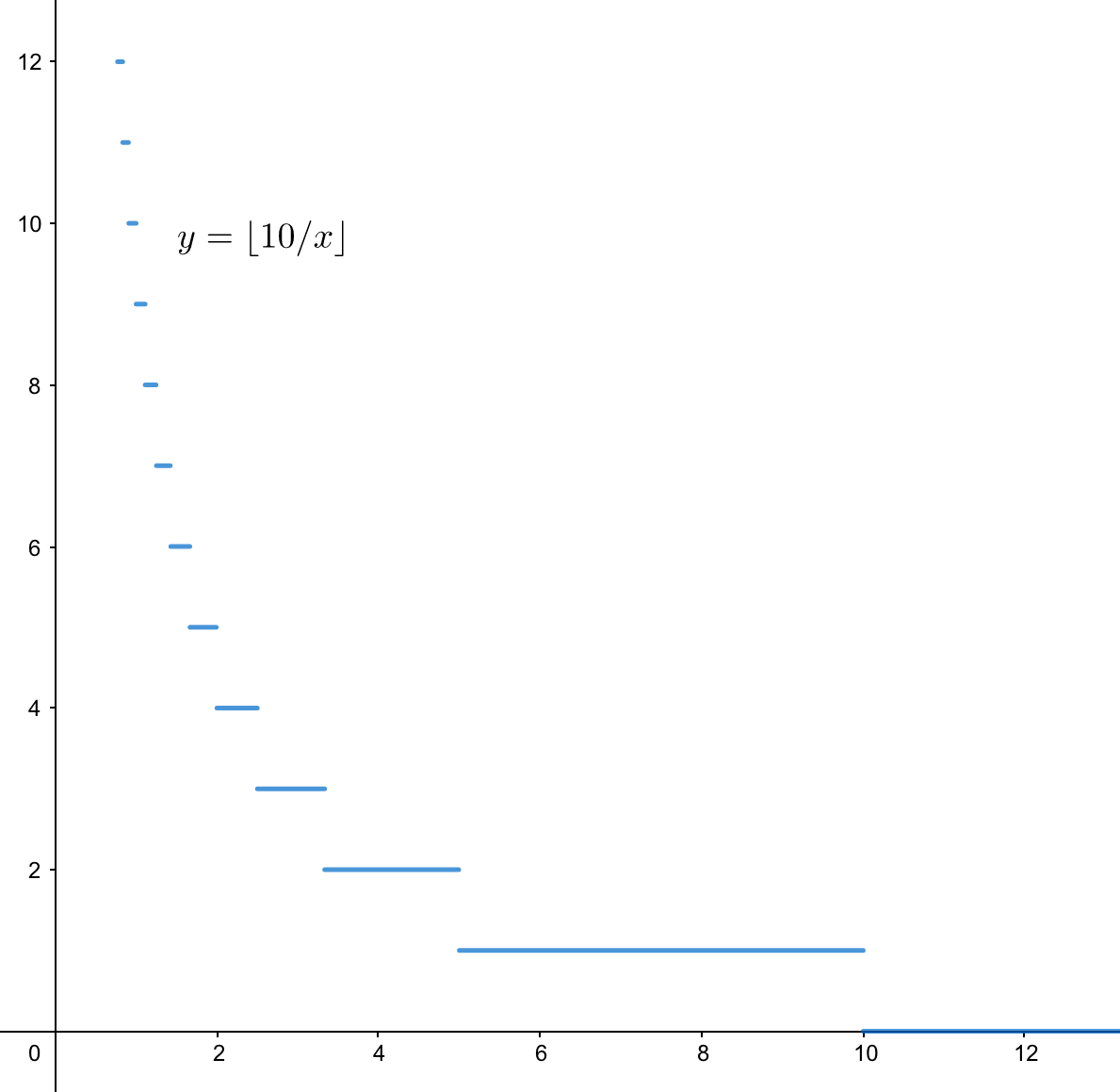
分块证明：

分段讨论：

• 当 $i\le \sqrt{k}$ 时，因为 $i$ 是 $[1,\sqrt{k}]$ 中的整数，所以只有 $\sqrt{k}$ 个不同的 $\lfloor {\displaystyle \frac{k}{i}}\rfloor$ 值。
• 当 $i>\sqrt{k}$ 时，$\lfloor {\displaystyle \frac{k}{i}}\rfloor \le \sqrt{k}$，又因为式子取整了，所以式子只能取到 $[1,\sqrt{k}]$ 的值，故最多也只有 $\sqrt{k}$ 个不同的 $\lfloor {\displaystyle \frac{k}{i}}\rfloor$ 值。

有关当 $i>\sqrt{k}$ 时，$\lfloor {\displaystyle \frac{k}{i}}\rfloor \le \sqrt{k}$ 的证明：

由于下取整，所以 $\lfloor {\displaystyle \frac{k}{i}}\rfloor \le k$，假设 $\lfloor {\displaystyle \frac{k}{i}}\rfloor >\sqrt{k}$，那么 $\lfloor {\displaystyle \frac{k}{i}}\rfloor \cdot \sqrt{k}>\sqrt{k^2}=k$，矛盾。

图和证明引自：墨染空

---

我们现在已经证明出了，可以将一段 长度为 $n$ 的序列分成 $2\sqrt{n}$ 段的序列，如果我们能做到 $O(1)$ 处理每一段，那么就可以将原先 $O(n^2)$ 的复杂度优化至 $O(n\sqrt{n})$。

假设有 $\lfloor {\displaystyle \frac{a}{x}}\rfloor$，假设此时的 $x$ 是下界，求能使这个值不变的，最大的 $x$ 为多少（上界），记这个上界是 $g(x)$。举个例子，$\lfloor {\displaystyle \frac{24}{9}}\rfloor$，值为 $2$，其中 $9$ 是下界，那么上界就是 $12$，因为 $\lfloor {\displaystyle \frac{24}{13}}\rfloor =1$。所以有 $\lfloor {\displaystyle \frac{a}{x}}\rfloor =\lfloor {\displaystyle \frac{a}{g(x)}}\rfloor$，且 $\lfloor {\displaystyle \frac{a}{g(x)}}\rfloor >\lfloor {\displaystyle \frac{a}{g(x)+1}}\rfloor$。这里的 $g(x)$ 实际上是有公式的：

$$g(x)=\lfloor {\displaystyle \frac{a}{\lfloor \frac{a}{x}\rfloor }}\rfloor$$

---

$g(x)$ 公式证明：

我们要证明的是 $\lfloor {\displaystyle \frac{a}{g(x)}}\rfloor =\lfloor {\displaystyle \frac{a}{x}}\rfloor$，且 $\lfloor {\displaystyle \frac{a}{x}}\rfloor >\lfloor {\displaystyle \frac{a}{g(x)+1}}\rfloor$，只有满足这个条件，才能证明 $g(x)$ 是使这个值不变的上界。

由于：

$$g(x)=\lfloor {\displaystyle \frac{a}{\lfloor \frac{a}{x}\rfloor }}\rfloor \ge \lfloor {\displaystyle \frac{a}{\frac{a}{x}}}\rfloor =\lfloor x\rfloor =x(x\in \mathbb{Z})$$

故 $g(x)\ge x$，所以 $\lfloor {\displaystyle \frac{a}{g(x)}}\rfloor \le \lfloor {\displaystyle \frac{a}{x}}\rfloor$。又因为

$$\lfloor {\displaystyle \frac{a}{\lfloor \frac{a}{\lfloor \frac{a}{x}\rfloor }\rfloor }}\rfloor \ge \lfloor {\displaystyle \frac{a}{\frac{a}{\lfloor \frac{a}{x}\rfloor }}}\rfloor =\lfloor {\displaystyle \frac{a}{x}}\rfloor$$

所以 $\lfloor {\displaystyle \frac{a}{g(x)}}\rfloor \ge \lfloor {\displaystyle \frac{a}{x}}\rfloor$，第一部分证毕。

用带余除法证明第二部分：

设 $a=kx+r$， 则 $0\le r<x$，并且用第一部分证得的结论，代入第二部分式子得：

$$\lfloor {\displaystyle \frac{a}{x}}\rfloor =k,\lfloor {\displaystyle \frac{a}{g(x)+1}}\rfloor =\lfloor {\displaystyle \frac{a}{\lfloor \frac{a}{k}\rfloor +1}}\rfloor$$

所以等价于证明

$$k>\lfloor {\displaystyle \frac{a}{\lfloor \frac{a}{k}\rfloor +1}}\rfloor ⟺\lfloor k\rfloor >\lfloor {\displaystyle \frac{a}{\lfloor \frac{a}{k}\rfloor +1}}\rfloor ,k\in \mathbb{Z}$$

等价于证明

$$k(\lfloor {\displaystyle \frac{a}{k}}\rfloor +1)>a$$

再令 $a=pk+q$，则 $0\le q<k$，等价于证明：

$$\begin{array}{rl}k(p+1)& >pk+q\\ kp+k& >pk+q\\ k& >q\end{array}$$

由于 $0\le q<k$，因此得证。

代码实现

// Author: CodeBoy

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define Re register
#define max(a, b) ((a) > (b) ? (a) : (b))
#define min(a, b) ((a) > (b) ? (b) : (a))
using namespace std;
typedef long long ll;
const int N = 50010;

int primes[N], cnt;
bool st[N];
int mobius[N], sum[N];

void init(int n)
{
    mobius[1] = 1;
    for (int i = 2; i <= n; i++)
    {
        if (!st[i])
        {
            primes[cnt++] = i;
            mobius[i] = -1;
        }
        for (int j = 0; primes[j] * i <= n; j++)
        {
            int t = primes[j] * i;
            st[t] = true;
            if (i % primes[j] == 0)
            {
                mobius[t] = 0;
                break;
            }
            mobius[t] = mobius[i] * -1;
        }
    }

    for (int i = 1; i <= n; i++)
        sum[i] = sum[i - 1] + mobius[i];
}

int main()
{
    init(N - 1);
    int t;
    scanf("%d", &t);
    while (t--)
    {
        int a, b, d;
        scanf("%d%d%d", &a, &b, &d);
        a /= d, b /= d;
        int n = min(a, b);
        ll res = 0;
        for (int l = 1, r; l <= n; l = r + 1)
        {
            r = min(n, min(a / (a / l), b / (b / l)));
            res += (sum[r] - sum[l - 1]) * (ll)(a / l) * (b / l);
        }
        printf("%lld\n", res);
    }

    return 0;
}