数组操作

题目

题面

给定一个长度为 $n$ 的整数数组。

数组中只包含 $1$ 和 $-1$。

你需要对该数组进行如下操作：

1. 计算该数组中所有元素的和 $s$。
2. 计算该数组的最小前缀和 $x$。
3. 输出 $s-x$ 的值。

注意：

1. 数组的最小前缀和 $x$ 有可能为负。
2. 对于任意数组，其前 $0$ 个元素的前缀和为 $0$。

输入格式

第一行包含整数 $n$。

第二行包含 $n$ 个整数，表示给定数组。

输出格式

一个整数，表示 $s-x$ 的值。

数据范围

前四个测试点满足 $1\le n\le 5$。
所有测试点满足 $1\le n\le 100$，数组中只包含 $1$ 和 $-1$。

输入样例1：

3
-1 -1 -1

输出样例1：

0

样例1解释

由给定数组，可以计算得到：

1. 给定数组内所有元素之和为 $-3$。
2. 给定数组的最小前缀和为 $-3$。

所以，答案为 $0$。

输入样例2：

4
1 1 1 1

输出样例2：

4

样例2解释

由给定数组，可以计算得到：

1. 给定数组内所有元素之和为 $4$。
2. 给定数组的最小前缀和为 $0$ （前 $0$ 个元素的前缀和）。

所以，答案为 $4$。

输入样例3：

2
-1 1

输出样例3：

1

输入样例4：

5
1 1 -1 1 1

输出样例4：

3

解析

签到水题, 只需记录前缀和最小值与元素总和即可, 最后不能忘记和0取最小值.

C++ 代码

//Author: CodeBoy
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
int a[1000];
int main(){
    int n;
    cin>>n;
    int s=0, x=0x3f3f3f3f;
    for(int i=0;i<n;i++){
        scanf("%d",&a[i]);
        s += a[i];
        x = min(s, x);
    }
    x = min(0, x);
    cout<<s-x<<endl;
    return 0;
}

减法操作

题目

题面

给定一个整数 $n$，执行如下算法：

1. 如果 $n=0$，则结束算法。
2. 找到 $n$ 的最小质因子 $d$。
3. 令 $n$ 减去 $d$ 并跳转步骤 $1$。

请你计算，在算法执行的过程中，一共进行了多少次减法操作。

输入格式

一个整数 $n$。

输出格式

一个整数，表示减法操作的次数。

数据范围

前三个测试点满足 $2\le n\le 5$。
所有测试点满足 $2\le n\le {10}^{10}$。

输入样例1：

5

输出样例1：

1

输入样例2：

4

输出样例2：

2

解析

(试除法) $O(\sqrt{n})$

因为质因数一定为奇数或$2$, 所以原数减去后一定为偶数, 接下来的最小质因子一定是$2$, 答案就是 ${\displaystyle \frac{n-factor}{2}}+1$

C++ 代码

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
ll get_minimum_factor(ll n){
    for(int i=2;i<=n/i;i++){
        if(n % i == 0) return i;
    }
    return n;
}
int main(){
    ll n;
    cin>>n;
    ll ans = 0;
    ll factor = get_minimum_factor(n);
    ans = (n-factor)/2 + 1;
    cout<<ans<<endl;
    return 0;
}

环形连通分量

题目

给定一个 $n$ 个点 $m$ 条边组成的无重边无自环的无向图。

请你计算，其包含的所有连通分量中，有多少个是环形的。

我们认为一个连通分量是环形的，当且仅当它的所有顶点重新排序后，可以满足：

• 第一个顶点通过一条边与第二个顶点相连。
• 第二个顶点通过一条边与第三个顶点相连。
• …
• 最后一个顶点通过一条边与第一个顶点相连。
• 所有上述提到的边各不相同。
• 连通分量中不包含除上述边以外的任何其他边。

根据定义，任何环形连通分量都至少包含三个顶点。

下面给出一个无向图示例。

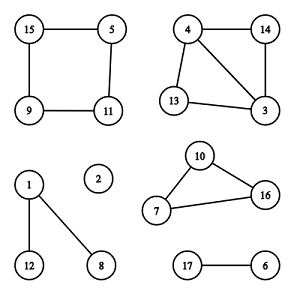
上面的无向图，一共包含 $6$ 个连通分量，其中有 $2$ 个连通分量是环形的：$[7,10,16]$ 和 $[5,11,9,15]$。

输入格式

第一行包含两个整数 $n,m$。

接下来 $m$ 行，每行包含两个整数 $u_i,v_i$，表示点 $u_i$ 和点 $v_i$ 之间存在一条无向边。

保证输入不存在重边和自环。

输出格式

一个整数，表示环形连通分量的数量。

数据范围

前五个测试点满足 $1\le n\le 20$，$0\le m\le 20$。
所有测试点满足 $1\le n\le 2\times {10}^5$，$0\le m\le 2\times {10}^5$，$1\le u_i,v_i\le n$，$u_i\ne v_i$。

输入样例1：

5 4
1 2
3 4
5 4
3 5

输出样例1：

1

输入样例2：

17 15
1 8
1 12
5 11
11 9
9 15
15 5
4 13
3 13
4 3
10 16
7 10
16 7
14 3
14 4
17 6

输出样例2：

2

解析

由题意知, 环形连通分量每个点度数一定为 $2$, 所以只需统计每个点的度数, 再用深搜找符合条件的联通块即可.

C++ 代码

//Author: CodeBoy

#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N = 2e5 + 5;
vector<int> g[N];
int deg[N], st[N];
bool flag;

void dfs(int u){
    
    st[u] = 1;
    for(auto x : g[u]){
        if(!st[x]){
            if(deg[x]!=2) flag = 1;
            dfs(x);
        }
    }
}

int main(){
    int n, m;
    cin>>n>>m;
    for(int i=0;i<m;i++){
        int a, b;
        cin>>a>>b;
        g[a].push_back(b);
        g[b].push_back(a);
        deg[a] ++, deg[b] ++;
    }

    int res = 0;

    for(int i=1;i<=n;i++){
        if(st[i]) continue;
        if(deg[i]!=2) continue;
        flag = 0;
        dfs(i);
        if(flag) continue;
        res ++;
    }
    cout<<res<<endl;
    return 0;
}