已知 $x+y+z=1$ 和 $x^2+y^2+z^2=1$, 求 $xyz$ 的最值 $M,m$

拉格朗日乘数法

拉格朗日乘数法对于这个问题非常有效. 首先观察到 $x=y=z$ 的情况不成立. 由对称性，我们可以假设 $z\ne x$ 且 $z\ne y$. 我们需要解以下方程组:

$$\mathrm{\nabla }(xyz)=\lambda \mathrm{\nabla }(x+y+z)+\mu \mathrm{\nabla }(x^2+y^2+z^2)$$

即，

$$\begin{array}{rl}yz& =\lambda +2\mu x\\ xz& =\lambda +2\mu y\\ xy& =\lambda +2\mu z\end{array}$$

从前两个方程中减去第三个方程，得到

$$\begin{array}{rl}y(z-x)& =-2\mu (z-x)\\ x(z-y)& =-2\mu (z-y)\end{array}$$

因此，$x=y$. 于是我们得到

$$2x+z=1,2x^2+z^2=1$$

这导致有两个解 $x=y=0,z=1$ 和 $x=y=\frac{2}{3},z=-\frac{1}{3}$. 因此，

$$M=0,m=\frac{2}{3}\cdot \frac{2}{3}\cdot (-\frac{1}{3})=-\frac{4}{27}$$

参数方程

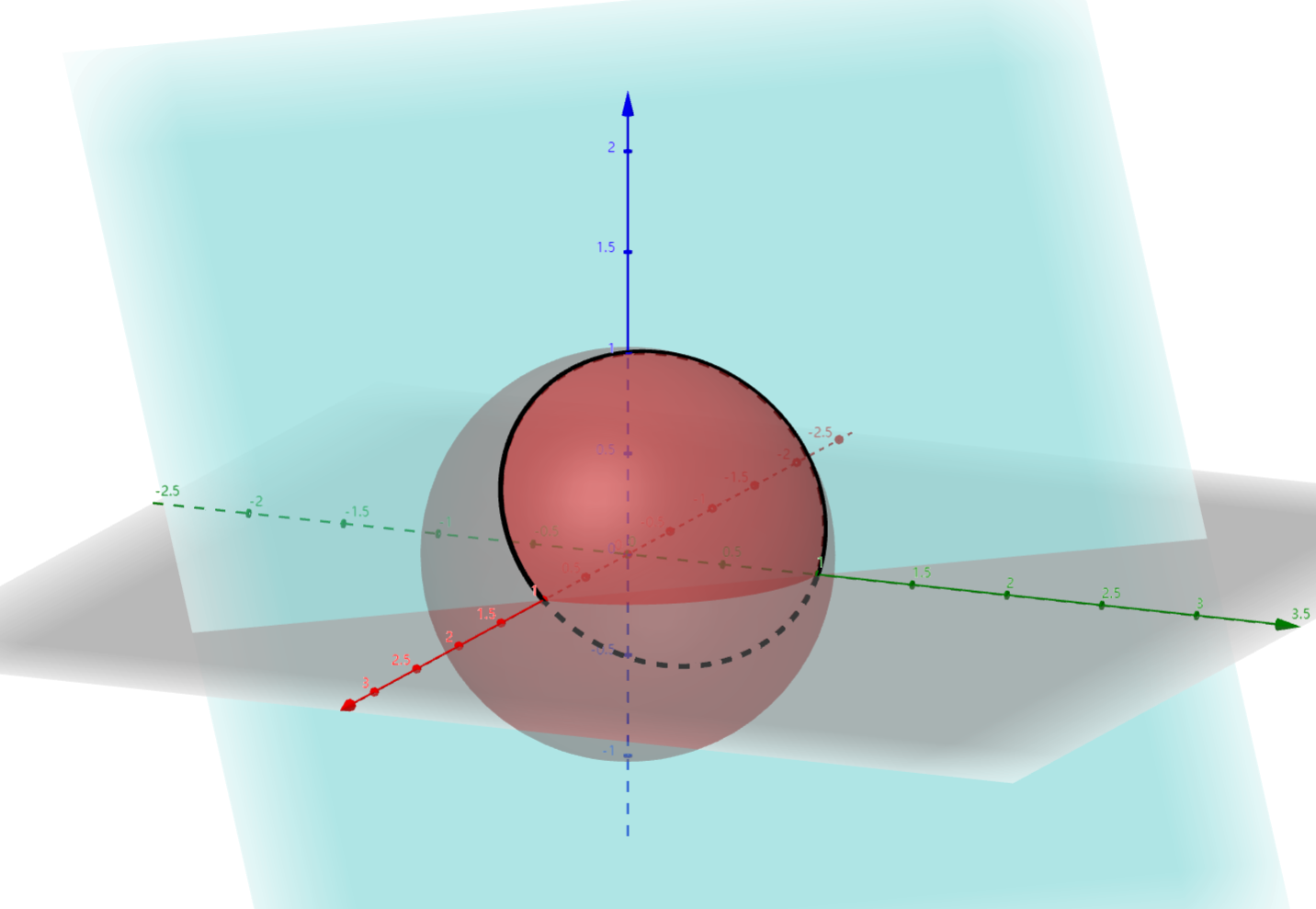
注意到球体和平面的交点产生了一个圆，可以用以下方程表示参数方程:

$$(\frac{1-\sqrt{3}\cos \left(t\right)+\sin \left(t\right)}{3},\frac{1+\sqrt{3}\cos \left(t\right)+\sin \left(t\right)}{3},\frac{1-2\sin \left(t\right)}{3})t\in [0,2\pi ].$$

现在将这个代入到给定的函数中，得到

$$f(t)=-\frac{2}{27}\cdot (4{\sin }^3(t)-3\sin \left(t\right)+1)=\frac{2}{27}\cdot (\sin \left(3t\right)-1)t\in [0,2\pi ]$$

这是一个单变量函数，可以简单地进行求出最值.

不等式

我们有 $z=1-x-y⟹f(x,y,z)=xyz=xy(1-x-y)=xy-xy(x+y)=g(x,y)$，满足 $x^2+y^2+(1-x-y{)}^2=1$

或 $2(x^2+y^2)-2x-2y+2xy=0$

或 $x^2+y^2-x-y+xy=0$

或 $(x+y{)}^2-xy-(x+y)=0$

$⟹g(x,y)=xy(1-(x+y))=((x+y{)}^2-(x+y))(1-(x+y))$

$=(x+y{)}^2-(x+y{)}^3-(x+y)+(x+y{)}^2=-t^3+2t^2-t,t=x+y$.

观察到: $(x+y{)}^2-(x+y)=xy\le {\displaystyle \frac{(x+y{)}^2}{4}}$

$⟹t^2-t\le {\displaystyle \frac{t^2}{4}}$

$⟹3t^2-4t\le 0$

$⟹t(3t-4)\le 0$

$⟹0\le t\le {\displaystyle \frac{4}{3}}.$

因此，问题转化为求 $h(t)=-t^3+2t^2-t,0\le t\le {\displaystyle \frac{4}{3}}$ 的最值.

有: $h^{\prime }(t)=-3t^2+4t-1=0⟹(-3t+1)(t-1)=0⟹t={\displaystyle \frac{1}{3}},1$.

在端点和关键点上评估 $h$: $h(0)=0,h(\frac{4}{3})=-{\displaystyle \frac{4}{27}},h(1)=0,h(\frac{1}{3})=-{\displaystyle \frac{4}{27}}$.

这表明最小值是 $-{\displaystyle \frac{4}{27}}$，最大值为 $0$.