普通快速选择算法

int quick_sort(int q[], int l, int r, int k)
{
    if (l >= r) return q[l];

    int i = l - 1, j = r + 1, x = q[l + r >> 1];
    while (i < j)
    {
        do i ++ ; while (q[i] < x);
        do j -- ; while (q[j] > x);
        if (i < j) swap(q[i], q[j]);
    }

    if (j - l + 1 >= k) return quick_sort(q, l, j, k);
    else return quick_sort(q, j + 1, r, k - (j - l + 1));
}

BFPRT

BFPRT 算法取基准值时采用 五划分中项 的方式，即中位数的中位数。

步骤实现

step1：将 $n$ 个元素每 $5$ 个一组，分成 $\lfloor \frac{n}{5}\rfloor$ 组，最后的一个组若不足 $5$ 个，直接舍去。
step2：取出每一组的中位数，最后一个组的不用计算中位数，任意排序方法，这里的数据比较少只有 $5$ 个，可以用简单的冒泡排序或是插入排序。
step3：将各组的中位数与数组开头的数据在组的顺序依次交换，这样各个组的中位数都排在了数据的左边。递归的调用中位数选择算法查找上一步中所有组的中位数的中位数，设为 $x$，偶数个中位数的情况下设定为选取中间小的一个。
step4：按照 $x$ 划分,大于或者等于 $x$ 的在右边,小于 $x$ 的在左边。
step5：step4 中划分后数据后返回一个下标 $i$，$i$ 左边的元素均是小于$x$，$i$ 右边的元素包括 $i$ 都是大于或是等于 x 的：

1.若 $i=k$，返回 $x$；
2.若 $i<k$，在小于 $x$ 的元素中递归查找第 $i$ 小的元素；
3.若 $i>k$，在大于等于 $x$ 的元素中递归查找第 $i-k$ 小的元素。

代码实现

¹

#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;

int n,m,k;
int a[1100000];

int ChooseSort(int left,int right);//选择排序，返回中位数下标
int BFPRT(int left,int right,int k);//求第k小，返回其位置的下标
int GetPivotIndex(int left,int right);//返回中位数的中位数下标
int Partition(int left,int right,int pivot_index);//利用中位数的中位数的下标进行划分，返回分界线下标

int ChooseSort(int left,int right)
//选择排序，返回中位数下标
{
    int temp;
    for(int i=left;i<right;i++)
    for(int j=i+1;j<=right;j++)
    {
        if(a[i]>a[j])swap(a[i],a[j]);
    }
    return(((right-left)/2)+left);
}

int GetPivotIndex(int left,int right)
 //返回中位数的中位数下标
{
    if (right-left<5)return(ChooseSort(left, right));

    int sub_right=left-1;
    for (int i=left;i+4<=right;i+=5)
    {
        int index=ChooseSort(i,i+4);  //找到五个元素的中位数的下标
        swap(a[++sub_right], a[index]);   //依次放在左侧
    }

    return BFPRT(left,sub_right,((sub_right-left+1)/2)+1);
}

int Partition(int left,int right,int pivot_index)
//利用中位数的中位数的下标进行划分，返回分界线下标
{
    swap(a[pivot_index],a[right]);  //把基准放置于末尾

    int divide_index=left;  //跟踪划分的分界线
    for (int i=left;i<right;i++)
    {
        if (a[i]<a[right])
            swap(a[divide_index++],a[i]);  //比基准小的都放在左侧
    }

    swap(a[divide_index], a[right]);  //最后把基准换回来
    return divide_index;
}

int BFPRT(int left,int right,int k)
//求第k小，返回其位置的下标
{
    int pivot_index=GetPivotIndex(left,right);//得到中位数的中位数下标
    int divide_index = Partition(left,right,pivot_index);//进行划分，返回划分边界
    int num=divide_index-left+1;
    if (num == k)return divide_index;
    else if (num>k)return BFPRT(left,divide_index-1,k);
    else return BFPRT(divide_index+1,right,k-num);
}

int main()
{
    scanf("%d%d",&n,&k);
    for(int i=1;i<=n;i++)scanf("%d",&a[i]);
    printf("%d",a[BFPRT(1,n,n-k+1)]);//第k大即第n-k+1小的数
    return 0;
}

复杂度分析

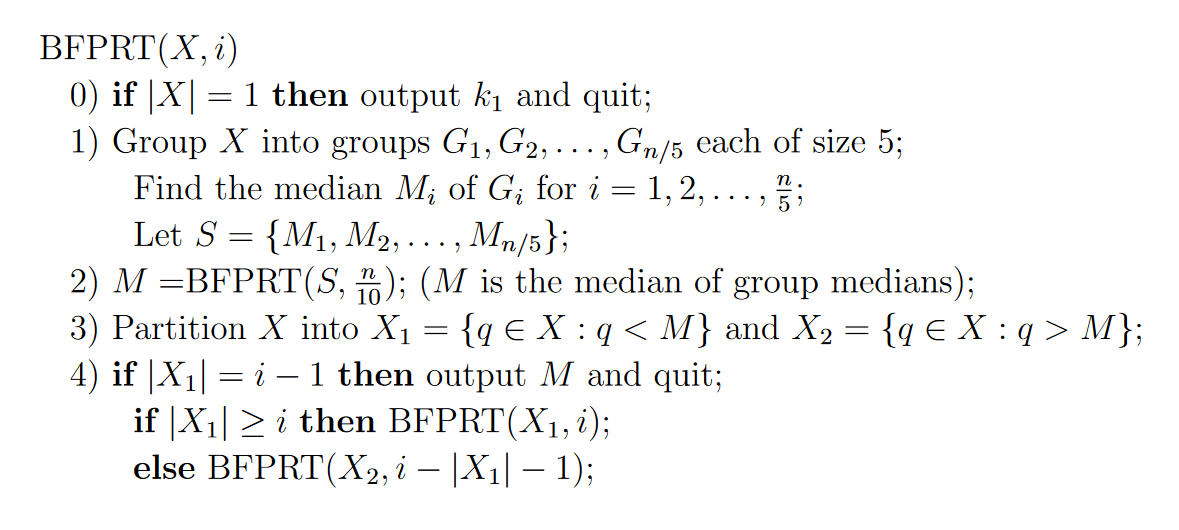
参考

• [1] 从快速排序到快速选择-BFPRT