求证: 对于所有的 , 成立
下面用几何法证明.
证明:
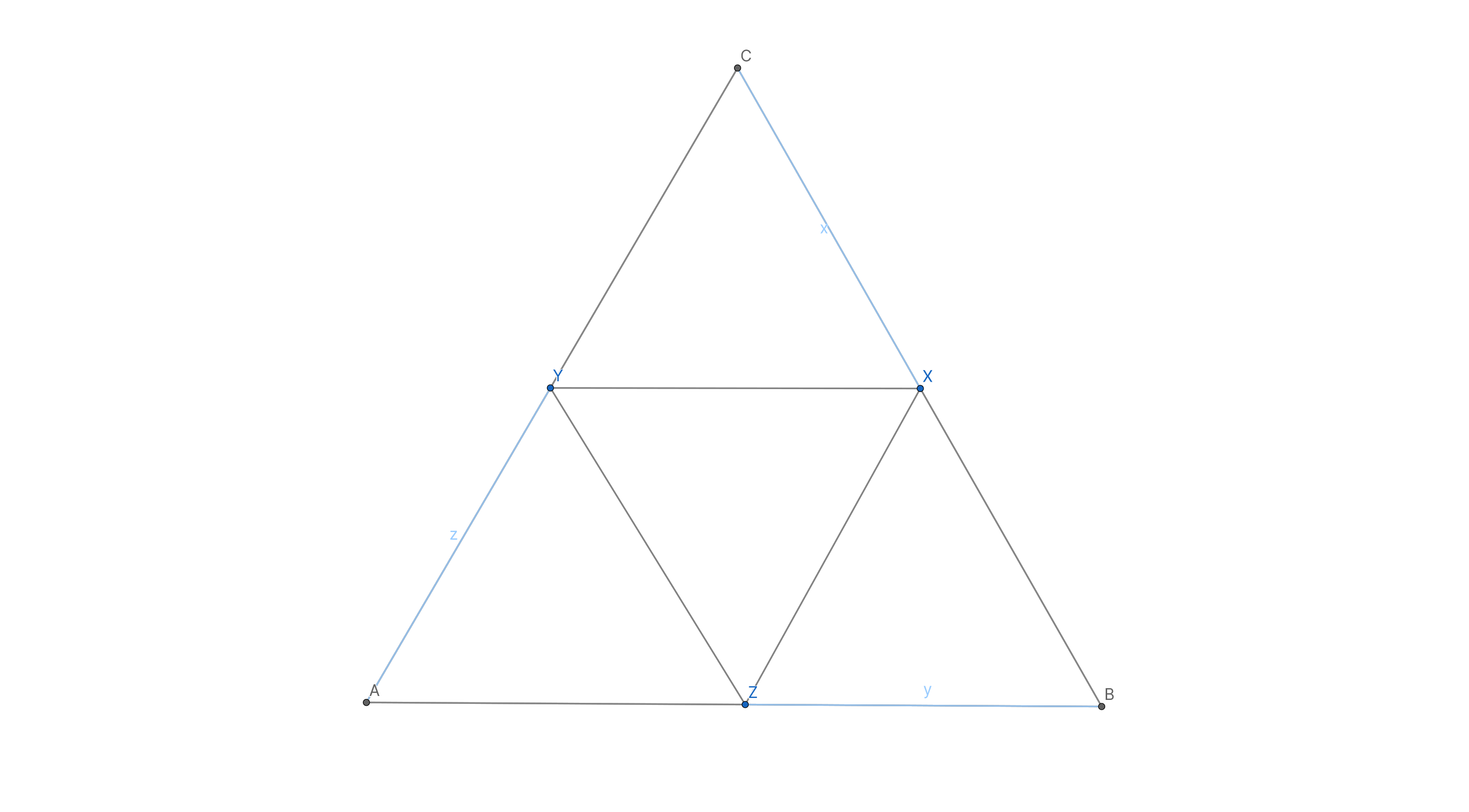
作边长为 的等边三角形 , 设点 分别在线段 上, 且 .
则有 $$\dfrac{S_{AYZ}+S_{BXZ}+S_{CXY}}{S_{ABC}}=x(1-z)+y(1-x)+z(1-y)$$
因为 , 即 .
这个证明来自 AoPS, 不过我认为 有问题, 只有当 时才能保证这个不等式成立, 也就是说, 在更一般的情况下, 有 , 即 , 而这是一个更强的结论.
所以这个优美的证明可以很容易扩展到下面的命题.
求证: 对于所有的 , 成立
证明:
引理1:
证明:
使用均值不等式
三式相加, 得 $$x^{2} + y^{2} + z^{2} \geq xy + xz + yz.$$
两边同时加上 , 即
展开原式得
右边可写成: .
. 当 时, 显然成立.
. 当 , 因为 , 所以也成立.
所以 $$x+y+z-xy-yz-xz\leq 1$$ 成立.
对于左边, 根据 引理1,
